一，引言

　　降维是对数据高维度特征的一种预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。在实际的生产和应用中，降维在一定的信息损失范围内，可以为我们节省大量的时间和成本。降维也成为了应用非常广泛的数据预处理方法。

　　降维具有如下一些优点：

（1）使得数据集更易使用

（2）降低算法的计算开销

（3）去除噪声

（4）使得结果容易理解

　　PCA(principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据压缩算法。在PCA中，数据从原来的坐标系转换到新的坐标系，由数据本身决定。转换坐标系时，以方差最大的方向作为坐标轴方向，因为数据的最大方差给出了数据的最重要的信息。第一个新坐标轴选择的是原始数据中方差最大的方法，第二个新坐标轴选择的是与第一个新坐标轴正交且方差次大的方向。重复该过程，重复次数为原始数据的特征维数。

　　通过这种方式获得的新的坐标系，我们发现，大部分方差都包含在前面几个坐标轴中，后面的坐标轴所含的方差几乎为0,。于是，我们可以忽略余下的坐标轴，只保留前面的几个含有绝不部分方差的坐标轴。事实上，这样也就相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，也就实现了对数据特征的降维处理。

　　那么，我们如何得到这些包含最大差异性的主成分方向呢？事实上，通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值及特征向量，选择特征值最大（也即包含方差最大）的N个特征所对应的特征向量组成的矩阵，我们就可以将数据矩阵转换到新的空间当中，实现数据特征的降维（N维）。

　　既然，说到了协方差矩阵，那么这里就简单说一下方差和协方差之间的关系，首先看一下均值，方差和协方差的计算公式：

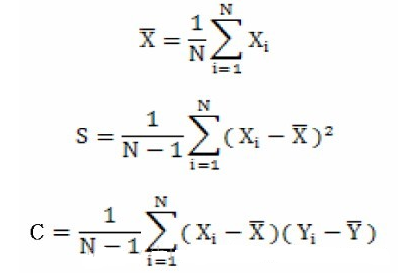
　由上面的公式，我们可以得到一下两点区别：

（1）方差的计算公式，我们知道方差的计算是针对一维特征，即针对同一特征不同样本的取值来进行计算得到；而协方差则必须要求至少满足二维特征。可以说方差就是协方差的特殊情况。　

（2）方差和协方差的除数是n-1，这样是为了得到方差和协方差的无偏估计。具体推导过程可以参见博文：http://blog.csdn.net/maoersong/article/details/21823397

二，PCA算法实现

　　将数据转换为只保留前N个主成分的特征空间的伪代码如下所示：

去除平均值计算协方差矩阵计算协方差矩阵的特征值和特征向量将特征值排序保留前N个最大的特征值对应的特征向量将数据转换到上面得到的N个特征向量构建的新空间中（实现了特征压缩）

　　具体的代码为：

#导入numpy库from numpy import *#解析文本数据函数#@filename 文件名txt#@delim 每一行不同特征数据之间的分隔方式，默认是tab键'\t'def loadDataSet(filename,delim='\t')    #打开文本文件    fr=open(filename)    #对文本中每一行的特征分隔开来，存入列表中，作为列表的某一行    #行中的每一列对应各个分隔开的特征    stringArr=[line.strip().split(delim) for line in fr.readlines()]    #利用map()函数，将列表中每一行的数据值映射为float型    datArr=[map(float.line)for line in stringArr]    #将float型数据值的列表转化为矩阵返回    return mat(datArr)#pca特征维度压缩函数#@dataMat 数据集矩阵#@topNfeat 需要保留的特征维度，即要压缩成的维度数，默认4096    def pca(dataMat,topNfeat=4096):    #求数据矩阵每一列的均值    meanVals=mean(dataMat,axis=0)    #数据矩阵每一列特征减去该列的特征均值    meanRemoved=dataMat-meanVals    #计算协方差矩阵，除数n-1是为了得到协方差的无偏估计    #cov(X,0) = cov(X) 除数是n-1(n为样本个数)    #cov(X,1) 除数是n    covMat=cov(meanRemoved,rowvar=0)    #计算协方差矩阵的特征值及对应的特征向量    #均保存在相应的矩阵中    eigVals,eigVects=linalg.eig(mat(conMat))    #sort():对特征值矩阵排序(由小到大)    #argsort():对特征值矩阵进行由小到大排序，返回对应排序后的索引    eigValInd=argsort(eigVals)    #从排序后的矩阵最后一个开始自下而上选取最大的N个特征值，返回其对应的索引    eigValInd=eigValInd[:-(topNfeat+1):-1]    #将特征值最大的N个特征值对应索引的特征向量提取出来，组成压缩矩阵    redEigVects=eigVects[:,eigValInd]    #将去除均值后的数据矩阵*压缩矩阵，转换到新的空间，使维度降低为N    lowDDataMat=meanRemoved*redEigVects    #利用降维后的矩阵反构出原数据矩阵(用作测试，可跟未压缩的原矩阵比对)    reconMat=(lowDDataMat*redEigVects.T)+meanVals    #返回压缩后的数据矩阵即该矩阵反构出原始数据矩阵    return lowDDataMat,reconMat

　　上述降维过程，首先根据数据矩阵的协方差的特征值和特征向量，得到最大的N个特征值对应的特征向量组成的矩阵，可以称之为压缩矩阵；得到了压缩矩阵之后，将去均值的数据矩阵乘以压缩矩阵，就实现了将原始数据特征转化为新的空间特征，进而使数据特征得到了压缩处理。

　　当然，我们也可以根据压缩矩阵和特征均值，反构得到原始数据矩阵，通过这样的方式可以用于调试和验证。

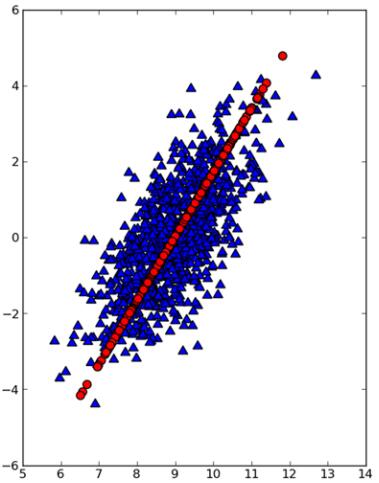
　　下图是通过matplotlib将原始数据点（三角形点）和第一主成分点（圆形点）绘制出来的结果。显然，第一主成分点占据着数据最重要的信息。

import matplotlibimport matplotlib.pyplot as pltfig=plt.figure()ax=fig.add_subplot(lll)#三角形表示原始数据点ax.scatter(dataMat[:,0].flatten().A[0],dataMat[:,1].flatten().A[0],\                    marker='^',s=90)#圆形点表示第一主成分点，点颜色为红色ax.scatter(reconMat[:,0].flatten().A[0],reconMat[:,1].flatten().A[0]\, marker='o',s=90,c='red')

三，示例：PCA对半导体数据进行降维

　　我们知道，像集成电路这样的半导体，成本非常昂贵。如果能在制造过程中尽早和尽快地检测出是否出现瑕疵，将可能为企业节省大量的成本和时间。那么，我们在面对大规模和高维度数据集时，显然计算损耗会很大，无疑会非常耗时。所以，如果利用PCA等降维技术将高维的数据特征进行降维处理，保留那些最重要的数据特征，舍弃那些可以忽略的特征，将大大加快我们的数据处理速度和计算损耗，为企业节省不小的时间和成本。

1 数据缺失值的问题

　　显然，数据集中可能会包含很多缺失值，这些缺失值是以NaN进行标识的。那么如何对待这些缺失值呢？如果存在大量的样本存在缺失值，显然选择将这些有缺失值得样本丢弃不可取；此外，由于并不知道这些值的意义，选择将缺失值替换为0也不是一个很好的决定。所以，这里我们选择将数据集中的特征缺失值，用数据集中该维度所有非NaN特征的均值进行替换。相比之下，采用均值替换的方法在这里是一个相对较好的选择。

#缺失值处理函数def replaceNaNWithMean():    #解析数据    datMat=loadDataSet('secom.data',' ')   #获取特征维度         numFeat=shape(datMat)[1]    #遍历数据集每一个维度    for i in range(numFeat):        #利用该维度所有非NaN特征求取均值        meanVal=mean(datMat[nonzero(~isnan(datMat[:,i].A))[0],i])        #将该维度中所有NaN特征全部用均值替换        datMat[nonzero(isnan(datMat[:,i].A))[0],i]=meanValreturn datMat

　　这样，我们就去除了所有NaN特征，接下来就可以对数据集利用PCA算法进行降维处理了。

2 PCA降维

　　那么我们如果确定需要保留哪些重要特征呢？PCA函数可以给出数据所包含的信息量，然后通过定量的计算数据中所包含的信息决定出保留特征的比例。下面是具体代码：

dataMat=pca.replaceNanWithMean()meanVals=mean(dataMat,axis=0)meanRemoved=dataMat-meanValsconMat=cov(meanRemoved,rowvar=0)eigVals,eigVects=linalg.eig(mat(covMat))

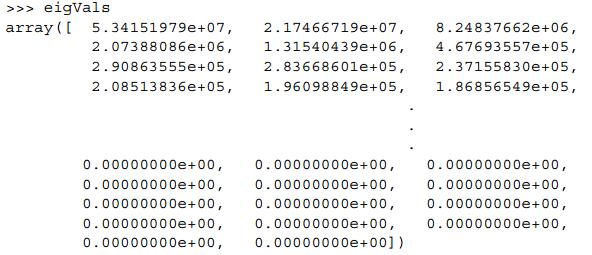
　　从上面的特征值结果，我们可以看到如下几个重要信息：

（1）里面有很多值都是0，这意味着这些特征都是其他特征的副本，都可以通过其他特征来表示，其本身没有提供额外的信息。

（2）可以看到最前面的15个特征值得数量级都大于10⁵，而后面的特征值都变得非常小。这表明，所有特征中只有部分特征是重要特征。

　　下图示出了数据集前20个主成分占总方差的百分比：

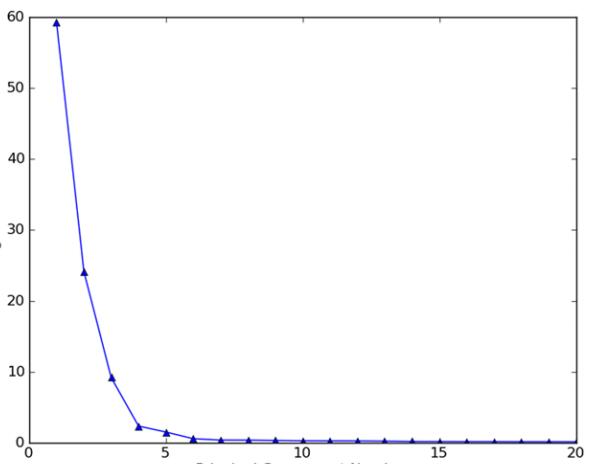
　　可以看出，数据的绝大部分方差都包含在前面的几个主成分中，舍弃后面的主成分并不会损失太多的信息。如果只保留前面几个最重要的主成分，那么在保留了绝大部分信息的基础上，可以将数据集特征压缩到一个非常低的程度，显然大大提高了计算效率。

　　下表是数据集前20个主成分所占的总方差百分比，以及累计方差百分比：

　　由上表可以看出，前六个主成分覆盖了数据96.8%的方差，前二十个主成分覆盖了99.3%的方差。这表明，通过特征值分析，我们可以确定出需要保留的主成分及其个数，在数据集整体信息（总方差）损失很小的情况下，我们可以实现数据的大幅度降维。

　　一旦，通过特征值分析知道了需要保留的主成分个数，那么我们就可以通过pca函数，设定合适的N值，使得函数最终将数据特征降低到最佳的维度。

四，总结

（1）降维是一种数据集预处理技术，往往在数据应用在其他算法之前使用，它可以去除掉数据的一些冗余信息和噪声，使数据变得更加简单高效，提高其他机器学习任务的计算效率。

（2）pca可以从数据中识别主要特征，通过将数据坐标轴旋转到数据角度上那些最重要的方向（方差最大）；然后通过特征值分析，确定出需要保留的主成分个数，舍弃其他主成分，从而实现数据的降维。